Published on Jun 05, 2023
Aerodynamics of Race Car
Race car performance depends on elements such as the engine, tires, suspension, road, aerodynamics, and of course the driver. In recent years, however, vehicle aero¬dynamics gained increased attention, mainly due to the utilization of the negative lift (downforce) principle, yielding several important performance improvements. This review briefly explains the significance of the aerodynamic downforce and how it improves race car performance. After this short introduction various methods to generate downforce such as inverted wings, diffusers, and vortex generators are dis¬cussed. Due to the complex geometry of these vehicles, the aerodynamic interaction between the various body components is significant, resulting in vortex flows and lifting surface shapes unlike traditional airplane wings. Typical design tools such as wind tunnel testing, computational fluid dynamics, and track testing, and their rel¬evance to race car development, are discussed as well. In spite of the tremendous progress of these design tools (due to better instrumentation, communication, and computational power), the fluid dynamic phenomenon is still highly nonlinear, and predicting the effect of a particular modification is not always trouble free. Several examples covering a wide range of vehicle shapes (e.g., from stock cars to open-wheel race cars) are presented to demonstrate this nonlinear nature of the flow field.
The motion of air around a moving vehicle affects all of its components in one form or another. Engine intake and cooling flow, internal ventilation, tire cooling, and overall external flow all fall under the umbrella of vehicle aerodynamics. The present discussion, however, focuses on the effects of external aerodynamics only, and ad¬ditional information on internal flows can be found in publications such as Hucho (1998, ch. 11-12). As mentioned earlier, the discussion on race car aerodynamics cannot be complete without briefly discussing tire characteristics. Although it is clear that airplanes fly on wings (hence the significance of aerodynamics), the fact that race cars "fly" on their tires is less obvious and requires additional clarification.
In fact aerodynamic forces can be used to improve tire adhesion and, thus, improve vehicle performance. For example, Figure 1 describes the forces acting on a side-slipping tire on the road. The right-hand side schematics depict the three forces (e.g., FX Fy FZ) acting on the tire in a Cartesian coordinate system aligned with the vehicle, and of course the three moments (Mx My MZ) must be included as well. In this case the vehicle is heading into the -x direction, but due to a positive side force (could be inertia due to cornering) it slides at an angle fi, as shown in the figure. Somewhat similar to the well-known dry friction model, a force is created by the tire, which is proportional to the normal force and initially varies linearly with the slip angle p.
How Downforce is Created
Race car design was historically always influenced by streamlining the vehicle body, particularly when the focus was on reducing high-speed air resistance. This trend continued well into the middle of the 1960s, implying that aerodynamic vehicles are also aesthetically attractive, an image that was somewhat altered by the discovery of aerodynamic downforce and its effect on race car performance. The foremost and simplest approach to generate downforce was to add inverted wings to the existing race cars. However, this newly discovered advantage was not free of complications. For example, the aerodynamic downforce increases with the square of the vehicle's speed whereas tires depend far less on speed. Consequently, if the inverted wings are attached to the vehicle then the suspension spring rate must be stiffened to allow for the additional high-speed loads. Variable downforce-generating devices followed, mostly based on reducing wing or flap angle of attack at higher speeds.
Another approach was to attach the wings to the unsprung suspension to avoid the stiffening of the suspension springs. These rapid developments within a short period (of less than a year) resulted in several catastrophic failures, followed by regulations completely outlawing movable aerodynamic devices. Some racing organizations ruled out even rotating cooling fans to eliminate any doubt about interpreting the meaning of "no movable aerodynamic device." But the addition of inverted wings was not the only method to generate downforce. Almost immediately it was realized that the vehicle body may be used to generate downforce as well. The main advantage is the large planview area of the vehicle, and therefore even small values of negative pressure under the vehicle can result in sizeable aerodynamic downforce. The answer to the heading of this section is that aerodynamic downforce can be generated by adding wings or by using the vehicle's body. Therefore, in the following paragraphs I discuss the principles of using attached wings and the various options for generating downforce with the vehicle body.
Race Car Wings
Airplane wing design matured by the middle of the twentieth century and it was only natural that race car designers borrowed successful airplane wing profiles to use on their vehicles. However, this approach was not entirely successful due to the inherent differences between these two applications. The difficulties in this technology transfer were highlighted by Katz (1994) and his findings can be summarized as follows:
A race car lifting surface design is different from a typical airplane wing design because (a) a race car's front wings operate within strong ground effect, (b) open-wheel race car rear wings have very small aspect ratio, and (f) there are strong interactions between the wings and other vehicle components (e.g., body, wheels, or other wings). These arguments are discussed in more detail in the following paragraphs.
Ground effect. The increase in the lift of an airplane's wing when approaching the ground was explained in the early stages of aerodynamic theory (e.g., Pistolesi 1935). The effect is favorable for both lifting and for inverted airfoils creating downforce. Typical results for an inverted airfoil are presented in Figure 3 (from Zerihan & Zhang 2000). The data clearly show the trend and the significant magnitude of the effect, particularly when the ground clearance is smaller than the airfoil quarter chord. The effect does not come freely and a similar increase in drag was measured by Zerihan & Zhang (2000). Because many race cars use front wings, typically mounted as close as h/c of 0.1-0.3, this principle is clearly utilized in race car design (in Figure 3, h = ground clearance and c = airfoil chord). In a later work, Zhang & Zerihan (2003) demonstrate the same obvious behavior for a wing with a two-element airfoil.
Because of the large magnitude of this effect, numerous studies focused on this subject and Coulliette & Plotkin (1996) recently summarized the two-dimensional effects. In their work they separated the contributions of parameters such as thickness, camber, and angle of attack to the airfoil's lift. From the race car point of view the interesting observation is that for an inverted airfoil (e.g., creating downforce) all of the above effects will increase the downforce near the ground.
Three-dimensional ground effect calculations for finite-span rectangular wings were reported by Katz 1985b, who showed that the effect remains large even in the case of an AR = 2 rectangular wing (which is less than most race car front wings). The focus of this study was on estimating the unsteady loads on such wings due to oscillatory heaving motions (due to suspension travel); this information was vital in those early days of using lifting surfaces on race cars. Because of the very close proximity to the ground, the type of boundary condition on the ground strongly affects both numerical and experimental results. Wiedemann (1989) discusses some of these effects and concludes that moving ground simulation is essential for such cases. He shows several types of boundary layers on the ground and Berndtsson et al. (1988) provide information on the floor boundary-layer flow, with or without rolling ground simulatio
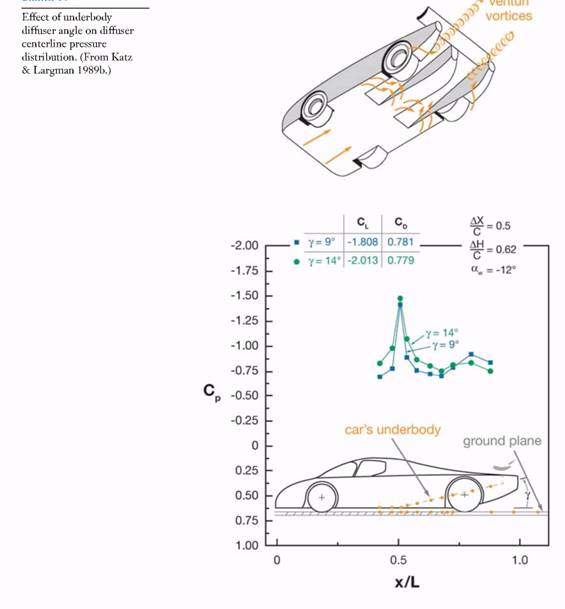
Add-Ons: Vortex Generators, Spoilers, Etc
In this section we discuss simple mod¬ifications that can be added to an existing car to increase downforce. One of the simplest add-ons is the vortex generator (VG). VGs were used for many years on aircraft, mainly to control boundary-layer flows. The size of VGs in such applications was on the order of the local boundary-layer thickness, and apart from influencing boundary-layer transition, they served to delay the flow separation on a wing's suction side. The use of such devices in automotive racing is quite different. Here the focus is on creating a stable and long-tip vortex, which in turn can reduce the pressure along its trail. A simple option is to add VGs at the front of the underbody and the long vortex trails of the VGs can induce low pressure under the vehicle. This principle is widely used for open-wheel race cars (e.g., Indy), and a typical integration of such VGs into the vehicle underbody.
In such an application the VG is much taller than the local boundary-layer thickness and the objective is to create a strong and stable vortex which, as noted, can generate suction loads along its trail. The principle was extensively used with delta winged aircraft at high angle of attack (Polhamus 1971), but when the wing surface was not at high angle of attack, the interest was mostly diminished (see, for example, Buchholz & Tso 2000). A generic study of these VGs mounted to flat plates was reported by Garcia & Katz (2003), and the results of a similar study, but with the actual shape of the race car underbody, was reported earlier by Katz & Garcia (2002). The combined downforce and drag results for the two underbody shapes is presented in Figure 14. Note that in the case of a flat plate the VGs were placed below the plate and ground clearance was measured from the lowest point of the VG to the ground. In the Indy-type under¬body case the VGs were flush with the immediately following body's lower surface and ground clearance was measured from the vehicle's or the VG's lower surface. Also, for the data in Figure 14 the VGs were oriented at 20-degyaw, and results for additional shapes and yaw angles are presented by Katz & Garcia (2002).
The downforce data in Figure 14, in general, increases as the ground clearance is reduced. The basic flat plate will have the lowest drag and no downforce. The curved Indy car underbody, but without the VGs, does generate downforce, even far from the ground, because of its effective thickness and camber. As ground proxim¬ity is reduced, downforce increases for this configuration, along with the associated drags.